NPTEL Introduction To Machine Learning – IITKGP Week 5 Assingnment Answers 2024
1.
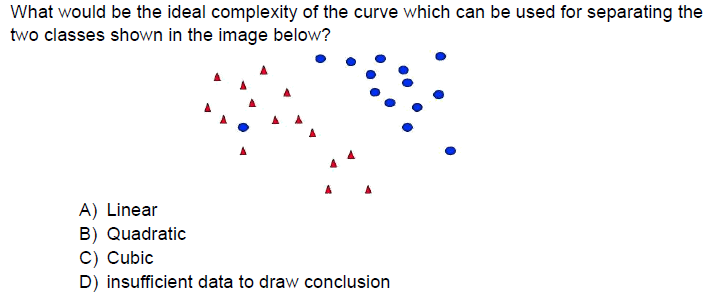
Answer :- For Answers Click Here
2. Suppose you have a dataset with n=10 features and m=1000 examples. After training a logistic regression classifier with gradient descent, you find that it has high training error and does not achieve the desired performance on training and validation sets. Which of the following might be promising steps to take?
- Create or add new polynomial features
- Use SVM with a non-linear kernel function
- Reduce the number of training examples
A) 1,2
B) 1, 3
C) 1,2, 3
D) None
Answer :- For Answers Click Here
3. In logistic regression, we learn the conditional distribution p(y|x), where y is the class label and x is a data point. If h(x) is the output of the logistic regression classifier for an input x, then P(y[x) equals:
A. h(x)y (1 – h(x)) (1-y)
B. h(x)y (1 + h(x))(1-y)
C. h(x) 1-y(1 – h(x))y
D. h(x)y(1 + h(x))(1+y)
Answer :- For Answers Click Here
4. The output of binary class logistic regression lies in the range:
A. [-1,01
B. [0,1]
C. [-1,-2)
D. [1,10]
Answer :-
5. State whether True or False.
“After training an SVM, we can discard all examples which are not support vectors and can still classity new examples.”
A) TRUE
B) FALSE
Answer :-
6. Suppose you are dealing with a 3-class classification problem and you want to train a SVM model on the data. For that you are using the One-vs-all method. How many times do we need to train our SVM model in such a case?
A) 1
B) 2
C) 3
D) 4
Answer :- For Answers Click Here
7. What is/are true about kernels in SVM?
- Kernel function can map low dimensional data to high dimensional space
- It’s a similarity function
A) 1
B) 2
C) 1 and 2
D) None of these.
Answer :-
8. If g(z) is the sigmoid function, then its derivative with respect to z may be written in term of g(z) as
A) g(2)(g(2)-1)
B) g(z)(1+g(z))
C) -g(z)(1+g(2))
D) g(z)(1-g(2)) |
Answer :-
9.
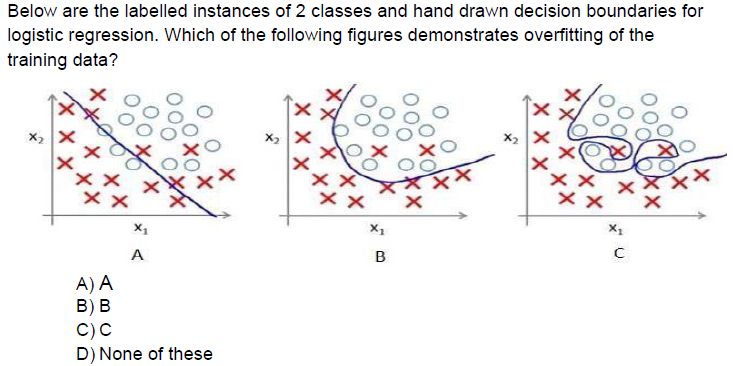
Answer :-
10. What do you conclude after seeing the visualization in the previous question (Question9)?
C1. The training error in the first plot is higher as compared to the second and third plot.
C2. The best model for this regression problem is the last (third) plot because it has minimum training error (zero).
C3. Out of the 3 models, the second model is expected to perform best on unseen data.
C4. All will perform similarly because we have not seen the test data.
A) C1 and C2
B) C1 and C3
C) C2 and C3
D) C4
Answer :- For Answers Click Here







