NPTEL Artificial Intelligence : Search Methods For Problem solving Week 6 Assignment Answers 2024
1. In the given map, which of the following heuristic functions satisfy the monotone condition?
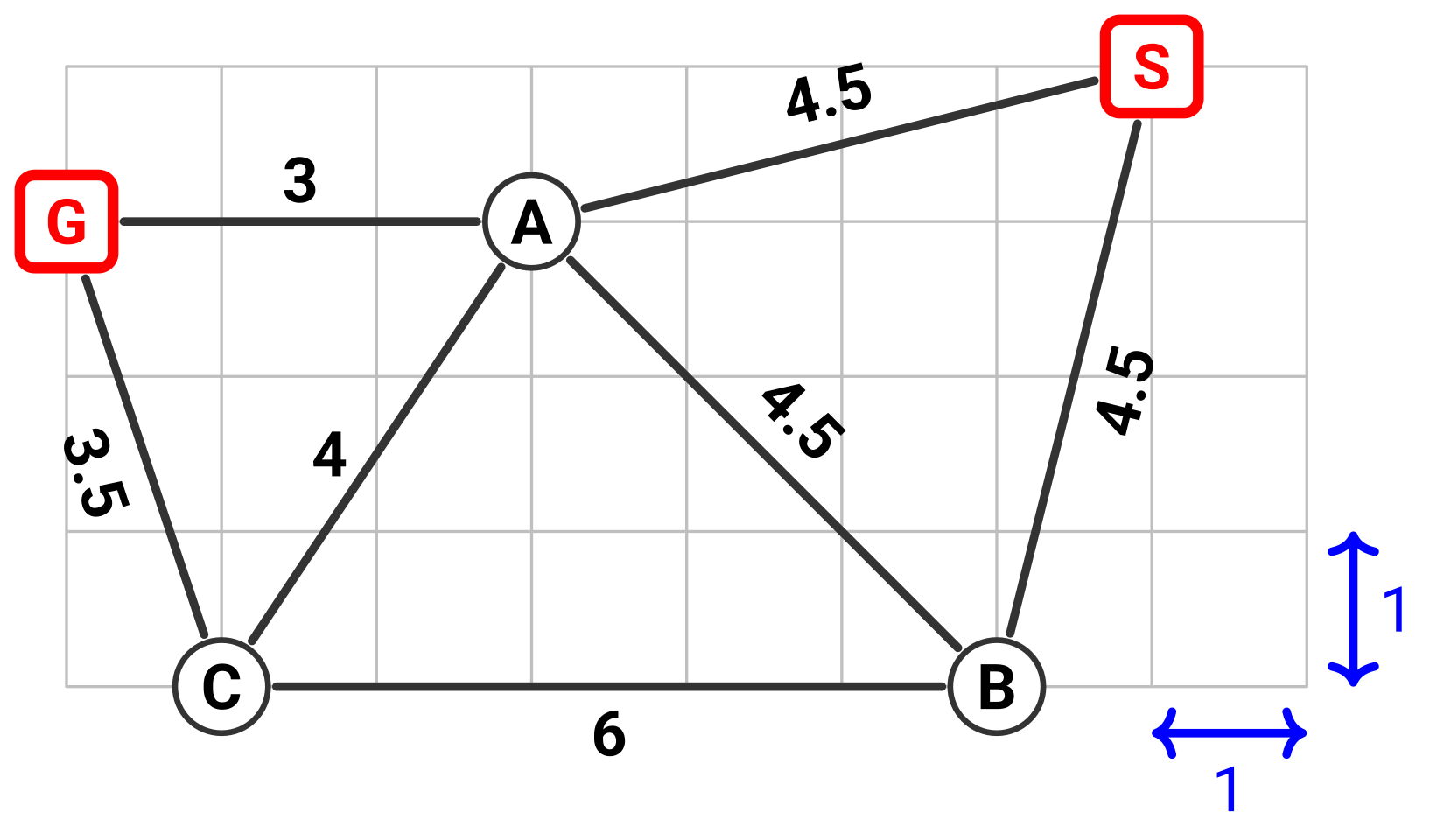
- Manhattan Distance
- Euclidean Distance
- (Manhattan Distance)/2
- None of the above
Answer :- For Answers Click Here
The figure (repeated from Week 5) shows a map on a grid where each tile is 10×10 in size. In this map, S is the start node and G is the goal node, the locations are connected by two-way edges (roads) where each edge has a cost that is the same in both directions.
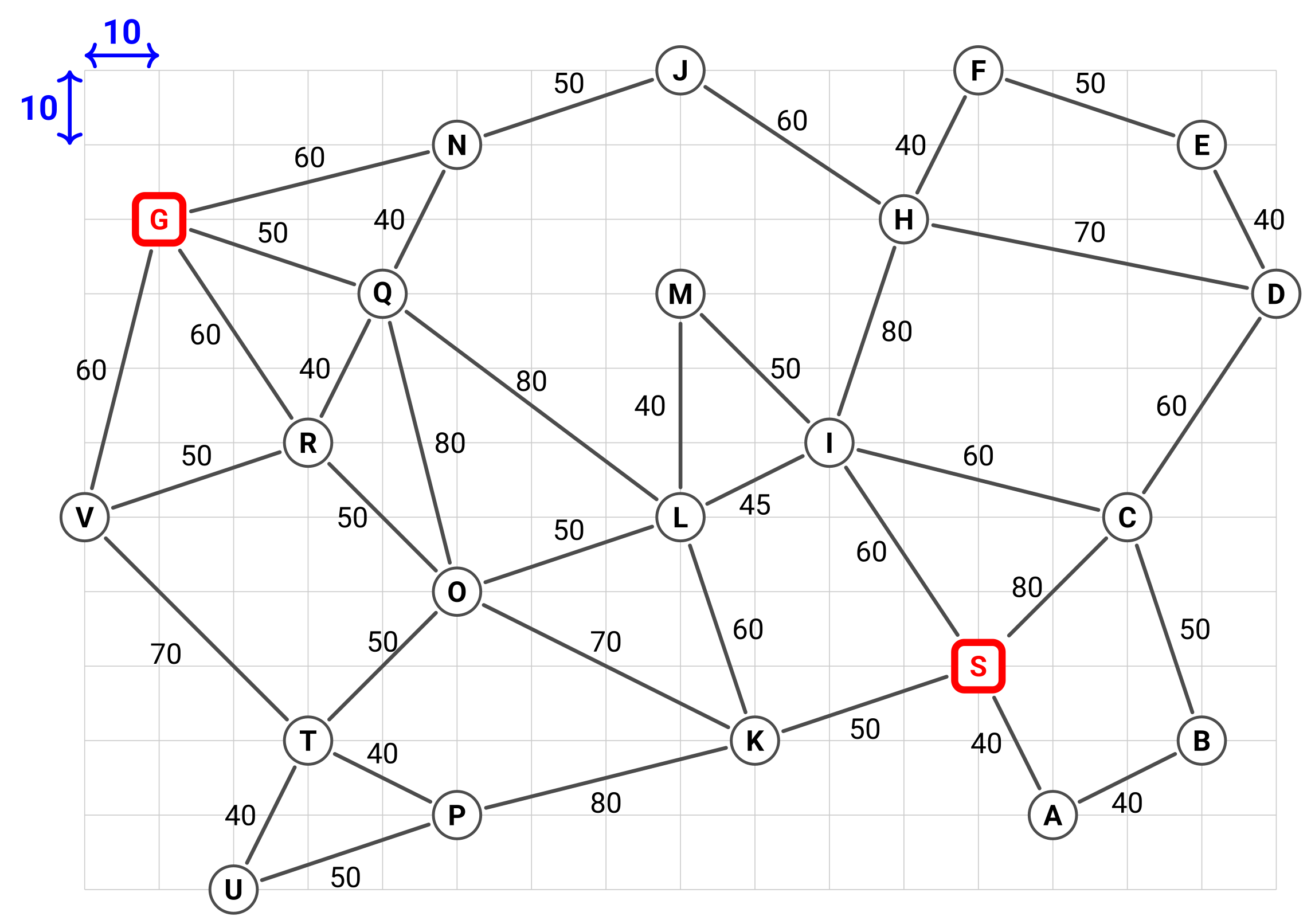
MoveGen returns nodes in alphabetical order.
Use Manhattan distance as the heuristic function.
Tie Breaker: when several nodes have the same cost, use alphabetical order to break ties.
Simulate wA* (w=2), Sparse-Memory Graph Search (SMGS), and Beam Search (beam width w=2) on the above map and then answer the following questions.
IMPORTANT: In assignments and exams, when we say a node is inspected (or expanded or refined) it means: the node is read from OPEN, then GoalTest is called, if it returns true then the node is processed as a goal, otherwise MoveGen is called and the neighbours are selectively placed in OPEN.
2. Simulate wA* (w=2) algorithm on the given map. Let S be the first node inspected, enter the 3rd, 4th and 5th node inspected by the algorithm.
Enter node labels.
Answer format: X,Y,Z
Answer :- For Answers Click Here
3. Enter the f-values of the 3rd, 4th and 5th nodes inspected by wA* algorithm.
Enter integers.
Answer format: 32,11,47
Answer :- For Answers Click Here
4. The path found by wA* algorithm is ________________ .
Answer :-
5. The cost of the path found by wA* algorithm is _________________ .
Answer :-
6. Let S be the first node inspected. After SMGS inspects the 3rd node, list the top 3 nodes (nodes with smaller f-values) in OPEN.
Enter the top 3 nodes
Enter NIL if the list is empty.
Answer format: X,Y,Z
Answer :- For Answers Click Here
7. After SMGS inspects the 3rd node, identify the BOUNDARY nodes and list them in ALPHABETICAL ORDER.
Answer :-
8. After SMGS inspects the 3rd node, identify the KERNEL nodes and list them in ALPHABETICAL ORDER.
Answer :-
9. After SMGS inspects the 6th node, list the top 3 nodes (nodes with smaller f-values) in OPEN. Enter the top 3 nodes.
Answer :-
10. After SMGS inspects the 6th node, identify the BOUNDARY nodes and list them in ALPHABETICAL ORDER.
Answer :- For Answers Click Here
11. After SMGS inspects the 6th node, identify the KERNEL nodes and list them in ALPHABETICAL ORDER.
Answer :-
12. After SMGS inspects the 8th node, list the top 3 nodes (nodes with smaller f-values) in OPEN. Enter the top 3 nodes.
Answer :-
13. After SMGS inspects the 8th node, identify the BOUNDARY nodes and list them in ALPHABETICAL ORDER.
Answer :-
14. After SMGS inspects the 8th node, identify the KERNEL nodes and list them in ALPHABETICAL ORDER.
Answer :- For Answers Click Here
15. Does the Beam Search algorithm (in Week 6 notes) allow duplicate nodes in a layer?
- Yes.
- No.
- Cannot be determined.
Answer :-
16. The start node S is added to the first layer in the beam. After expanding the first layer, the 2nd layer is formed. List the nodes in the 2nd layer.
Enter the nodes in ALPHABETICAL ORDER.
Enter NIL if the layer is empty.
Answer format: A,B,C
Answer :-
17. List the nodes in the 3rd layer.
Enter the nodes in ALPHABETICAL ORDER.
Enter NIL if the layer is empty.
Answer format: A,B,C
Answer :- For Answers Click Here
18. Path found by the Beam Search algorithm is _________________ .
Answer :-
19. The cost of the path found by Beam Search is _______________ .
Answer :-
20. For a finite state space with finite edge costs and having paths from start to goal, which of the following algorithms are likely to find sub optimal paths from start to goal?
- A* with admissible heuristic
- A* with inadmissible heuristic
- Beam Search
- Best First Search
- Branch and Bound
- Breadth First Search
- Depth First Search
- Hill Climbing
- SMGS with admissible heuristic
- SMGS with inadmissible heuristic
Answer :- For Answers Click Here







