NPTEL Introduction To Machine Learning – IITKGP Week 4 Assignment Answers 2024
1. A man is known to speak the truth 2 out of 3 times. He throws a die and reports that the number obtained is 4. Find the probability that the number obtained is actually 4 :
A. 2/3
B. 3/4
C. 5/22
D. 2/7
Answer :- d
2. Two cards are drawn at random from a deck of 52 cards without replacement. What is the probability of drawing a 2 and an Ace in that order?
A. 4/51
B. 1/13
C. 4/256
D. 4/663
Answer :- d
3.
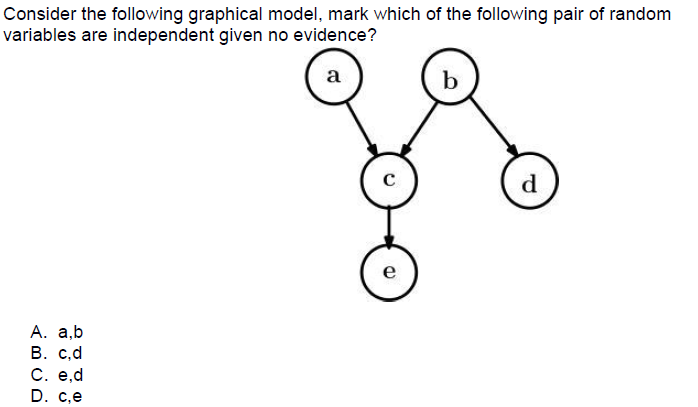
Answer :- For Answer Click Here
4.
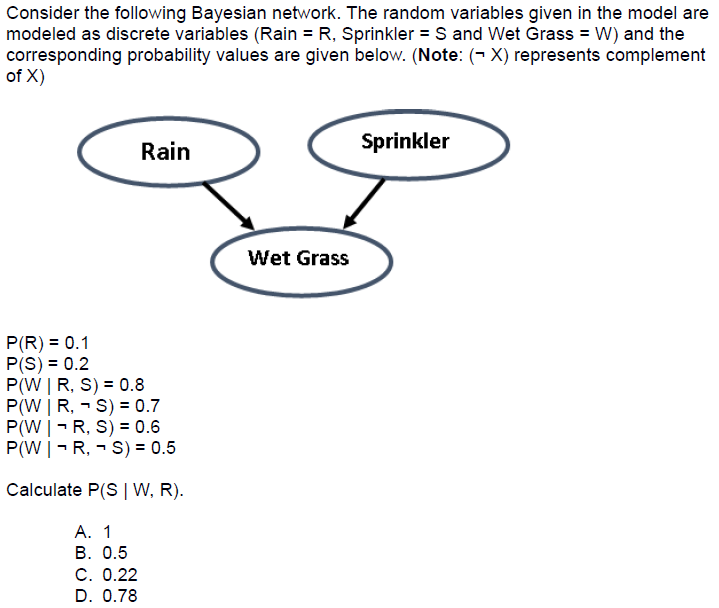
Answer :- For Answer Click Here
5. What is the naive assumption in a Naive Bayes Classifier?
A. All the classes are independent of each other
B. All the features of a class are independent of each other
C. The most probable feature for a class is the most important feature to be considered for classification
D. All the features of a class are conditionally dependent on each other.
Answer :-
6. A drug test (random variable T) has 1% false positives (i.e., 1% of those not taking drugs show positive in the test), and 5% false negatives (i.e.., 5% of those taking drugs test negative). Suppose that 2% of those tested are taking drugs. Determine the probability that somebody who tests positive is actually taking drugs (random variable D).
A. 0.66
B. 0.34
C. 0.50
D. 0.91
Answer :-
7. It is given that P(A|B) = 2/3 and P(A|B) = 1/4. Compute the value of P(B|A).
A. ½
B. ⅔
C. ¾
D. Not enough information.
Answer :- For Answer Click Here
8.

Answer :-
9. Bag | contains 4 white and 6 black balls while another Bag Il contains 4 white and 3 black balls. One ball is drawn at random from one of the bags and it is found to be black. Find the probability that it was drawn from Bag I.
A. 1/2
B. 2/3
C. 7/12
D. 9/23
Answer :-
10. In a Bayesian network a node with only outgoing edge(s) represents
A. a variable conditionally independent of the other variables.
B. a variable dependent on its siblings.
C. a variable whose dependency is uncertain.
D. None of the above.
Answer :- For Answer Click Here
NPTEL Introduction To Machine Learning – IITKGP Week 4 Assignment Answers 2023
Questions 1-4 with the data provided below:
A spam filtering system has a probability of 0.95 to classify correctly a mail as spam and 0.10
probability of giving false positives. It is estimated that 0.5% of the mails are actual spam
mails.
Q1) Suppose that the system is now given a new mail to be classified as spam/ not-spam, what is the probability that the mail will be classified as spam?
a. 0.89575
b. 0.10425
c. 0.00475
d. 0.09950
Answer:- b
Q2. Find the probability that, given a mail classified as spam by the system, the mail actually being spam.
a. 0.04556
b. 0.95444
c. 0.00475
d. 0.99525
Answer:- For Answer Click Here
Q3. Given that a mail is classified as not spam, the probability of the mail actually being not spam
a. 0.10425
b. 0.89575
c. 0.003
d. 0.997
Answer:-
Q4. Find the probability that the mail is misclassified:
a. 0.90025
b. 0.09975
c. 0.8955
d. 0.1045
Answer:- For Answer Click Here
Q5. What is the naive assumption in a Naive Bayes Classifier?
a. All the classes are independent of each other
b. All the features of a class are independent of each other
c. The most probable feature for a class is the most important feature to be considered for classification
d. All the features of a class are conditionally dependent on each other.
Answer:-

Q6.

Answer:- For Answer Click Here
Q7. Find P (K=0| a=1, b=1).
a. 1/3
b. 2/3
C. 1/9
d. 8/9
Answer:-

Q8. What is the joint probability distribution in terms of conditional probabilities?
a. P(D1) * P(D2\D1) * P(S1|D1) * P(S2]D1) * P(S3|D2)
b. P(D1) * P(D2) * P(S1\D1) * P(S2]D1) * P(S3|D1, D2)
c. P(D1) * P(D2) * P(S1 D2) * P(S2]D2) * P(S3|D2)
d. P(D1) * P(D2) * P(S1|D1) * P(S2|D1, D2) * P(S3|D2)
Answer:- For Answer Click Here
Q9. Suppose P(D1) = 0.4, P(D2) = 0.7 , P(SID1)=0.3 and P(S1| D1′)= 0.6. Find P(S1)
a. 0.12
b. 0.48
c. 0.36
d. 0.60
Answer:-
Q10. What is the Markov blanket of variable, S3
a. D1
b. D2
c. D1 and D2
d. None
Answer:- For Answer Click Here
Q11.

Answer:-
Q12.

Answer:-
Questions 13-14 with the data given below:
In an oral exam you have to solve exactly one problem, which might be one of three types, A. B, or C, which will come up with probabilities 30%, 20%, and 50%, respectively. During your preparation you have solved 9 of 10 problems of type A. 2 of 10 problems of type B, and 6 of 10 problems of type C.
13) What is the probability that you will solve the problem of the exam?
а. 0.61
b. 0.39
c. 0.50
d. 0.20
Answer:- For Answer Click Here
Q14. Given you have solved the problem, what is the probability that it was of type A?
а. 0.35
b. 0.50
c. 0.56
d. 0.44
Answer:-
Q15. Naive Bayes is a popular classification algorithm in machine learning. Which of the
following statements is/are true about Naive Bayes?
a. Naive Bayes assumes that all features are independent of each other, given the class.
b. It is particularly well-suited for text classification tasks, like spam detection.
c. Naive Bayes can handle missing values in the dataset without any special treatment.
d. It is a complex algorithm that requires a large amount of training data.
Answer:-






